
Fyzika
je přírodní věda, která popisuje přírodní děje a základní vlastnosti přírody.
Fyzika používá teoretické a experimentální metody. Má velký význam pro rozvoj
techniky a stává se tak důležitým nástrojem růstu životní úrovně. Má také
důležitý světonázorový význam.
Experimentální a teoretická fyzika

Metody fyziky vychází z pozorování pokusů. Indukcí dospívá fyzika k obecným zákonům. Z nich dedukcí předpoví výsledek dalšího pokusu a jeho praktickým provedením platnost zákona potvrzuje.
Fyzikální veličina udává kvalitativní popis určité fyzikální vlastnosti nebo děje, je to například hmotnost, délka, rychlost ...
Fyzikální jednotka popisuje fyzikální veličinu kvantitativně, je mírou fyzikální veličiny. Např.: fyzikální jednotkou hmotnosti je kilogram, délky metr, rychlosti metr za sekundu, ... a vyjadřuje velikost fyzikální veličiny, používáme ji k měření.
Jedná se o mezinárodně používanou soustavu jednotek. Jako každá jiná soustava fyzikálních veličin a jednotek používá několik (7) základních veličin a jednotek,
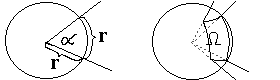 radián rad jako jednotka rovinného
úhlu
radián rad jako jednotka rovinného
úhlu 
| Předpona | Značka | Násobek | Příklad |
| tera- | T | 1012 = 1 000 000 000 000 | T |
| giga- | G | 109 = 1 000 000 000 | GW = gigawatt |
| mega- | M | 106 = 1 000 000 | MV = megavolt |
| kilo- | k | 103 = 1 000 | km = kilometr |
| mili- | m | 10-3 = 0.001 | mA = miliampér |
| mikro- | 10-6 = 0.000 001 | µs = mikrosekunda | |
| nano- | n | 10-9 = 0.000 000 001 | nm = nanometr |
| piko- | p | 10-12 | pF = pikofarad |
| femto- | f | 10-15 | |
| atto- | a | 10-18 | |
| Základní veličina | značka veličiny | Základní jednotka | značka jednotky |
| délka | l | metr | m |
| hmotnost | m | kilogram | kg |
| čas | t | sekunda | s |
| elektrický proud | I | ampér | A |
| termodynamická teplota | T | kelvin | K |
| látkové množství | n | mol | mol |
| svítivost | I | kandela | cd |
Žádné měření nemůže být absolutně přesné, vždy je zatíženo chybou měření. Velikost fyzikální veličiny
obvykle určujeme jako aritmetický průměr několika měření. Podle rozdílů
mezi naměřenými hodnotami můžeme usuzovat na přesnost resp. chybu měření.
Např.: měřením získáme 5 hodnot délky (viz tabulka). Ve druhém sloupci tabulky
jsou odchylky jednotlivých měření od aritmetického průměru. Průměrná odchylka (z
absolutních hodnot) udává chybu měření, určuje interval, ve kterém leží
měřená fyzikální veličina s velkou pravděpodobností (pravděpodobnost závisí na
počtu měření).
Příklad tabulky měření délky l
| číslo měření |
l mm |
mm |
| 1 | 18 | -0,4 |
| 2 | 16 | 1,6 |
| 3 | 19 | -1,4 |
| 4 | 17 | 0,6 |
| 5 | 18 | -0,4 |
| průměr | 17,6 | 0,88 |
Výpočty ![]() =(18+16+19+17+18)/5=17,6
=(18+16+19+17+18)/5=17,6
![]() l = (0,4 + 1,6 + 1,4 + 0,6 + 0,4)/5 = 0,88
l = (0,4 + 1,6 + 1,4 + 0,6 + 0,4)/5 = 0,88
![]() l =
l = ![]() l/
l/![]() = 0,05 = 5%
= 0,05 = 5%
Zápis výsledku
l = ![]()
![]()
![]() l ... s relativní odchylkou
l ... s relativní odchylkou ![]() l znamená, že:
l znamená, že:
l ![]() < l-
< l-![]() l , l+
l , l+![]() l> (Výsledek vhodně
zaokrouhlíme) tedy:
l> (Výsledek vhodně
zaokrouhlíme) tedy:
l = (17,6 ![]() 0,9) mm s relativní odchylkou
5%,
0,9) mm s relativní odchylkou
5%,
l ![]() < 16,7 ; 18,5 >
< 16,7 ; 18,5 >
mohou být systematické
a hrubé (ty mohou být
odstraněny) a chyby náhodné (ty charakterizují přesnost měření).
Průměrná odchylka ![]() (ve středoškolském
kurzu nahrazuje tzv. střední kvadratickou chybu
(ve středoškolském
kurzu nahrazuje tzv. střední kvadratickou chybu ![]() ) je určena jako aritmetický průměr všech odchylek (jejich absolutních
hodnot) od aritmetického průměru měřené veličiny. Relativní odchylka
) je určena jako aritmetický průměr všech odchylek (jejich absolutních
hodnot) od aritmetického průměru měřené veličiny. Relativní odchylka ![]() (ve středoškolském kurzu nahrazuje relativní
chybu
(ve středoškolském kurzu nahrazuje relativní
chybu ![]() ) je průměrná odchylka
vyjádřená obvykle v procentech vzhledem k aritmetickému průměru měřené veličiny
(viz předchozí příklad).
) je průměrná odchylka
vyjádřená obvykle v procentech vzhledem k aritmetickému průměru měřené veličiny
(viz předchozí příklad).
Chyby můžeme také určovat odhadem. Za průměrnou odchylku pak považujeme polovinu nejmenšího dílku dělení stupnice použitého měřidla.
Jestliže výslednou hodnotu fyzikální veličiny určujeme výpočtem z
naměřených veličin, jejichž odchylky známe, postupujeme tak, že:
průměrnou odchylku součtu (nebo rozdílu) veličin určíme jako součet
odchylek měřených veličin a relativní odchylku dopočteme z průměrné odchylky,
x = a ![]() b,
b, ![]() x =
x = ![]() a +
a + ![]() b,
b, ![]() a =
a = ![]() a/a
a/a
relativní odchylku součinu (nebo podílu) veličin určíme jako součet
relativních odchylek měřených veličin a průměrnou odchylku dopočteme z výsledné
relativní odchylky.
x = a.b (nebo x = a/b),![]() x =
x = ![]() a +
a + ![]() b,
b, ![]() a = a.
a = a.![]() a
a
- kinematika - se zabývá
popisem pohybu hmotného bodu v prostoru a čase. Těleso a hmotný bod jsou myšlenkové modely
skutečných objektů. Určování polohy -
provádíme vždy relativně
vzhledem kjinému tělesu nejčastěji pomocí souřadnic ve vztažné soustavě. 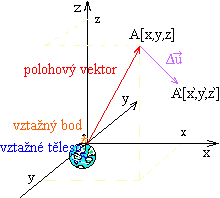 Polohový vektor velmi dobře popisuje polohu tělesa. Je
to vektor, který má počátek v
počátku systému souřadnic a koncový bod v místě polohy popisovaného tělesa.
Změnu polohy pak dobře popisuje změna polohového vektoru (což je opět vektor - od
bodu A do A'). Vztažná soustava je tvořena vztažným tělesem se vztažným bodem (od toho měříme
souřadnice) a soustavou souřadnic. Nejčastěji používáme pravoúhlou soustavu
souřadnic. Poloha bodu v prostoru je tak jednoznačně určena souřadnicemi x, y, z.
Polohový vektor velmi dobře popisuje polohu tělesa. Je
to vektor, který má počátek v
počátku systému souřadnic a koncový bod v místě polohy popisovaného tělesa.
Změnu polohy pak dobře popisuje změna polohového vektoru (což je opět vektor - od
bodu A do A'). Vztažná soustava je tvořena vztažným tělesem se vztažným bodem (od toho měříme
souřadnice) a soustavou souřadnic. Nejčastěji používáme pravoúhlou soustavu
souřadnic. Poloha bodu v prostoru je tak jednoznačně určena souřadnicemi x, y, z.
Popis pohybu
Mechanický pohyb je změna polohy v prostoru a čase. Pohyb a klid můžeme popisovat vždy jen relativně (ve vztahu k jinému tělesu). Absolutní pohyb a klid je objektivně nezjistitelný.
 K relativitě rychlosti
K relativitě rychlosti
Vzhledem ke Šmudlovi jede Jánošík rychlostí v1, avšak vzhledem k Bílému
Tesákovi jede rychlostí v1 - v2. Vzhledem ke Šmudlovi se Slimouš
pohybuje rychlostí v2. Vzhledem k Bílému Tesákovi se Slimouš nepohybuje
vůbec.
Skalární veličiny - (např.: hmotnost, práce, ...) jsou ty, které jsou úplně určeny svou velikostí. Určujeme je reálným číslem.
Vektorové veličiny - (např.: síla, rychlost, ...) jsou určeny svou velikostí a směrem. Vektory znázorňujeme pomocí šipky, její délka znázorňuje velikost veličiny, směr šipky znázorňuje směr popisované veličiny. Vektor můžeme určit i pomocí souřadnic. (Vektor směřující z počátku systému souřadnic do bodu A má souřadnice bodu A. Souřadnicemi je jednoznačně určena velikost vektoru i jeho směr. Umístění vektoru může být libovolné. V některých případech může na umístění vektoru záležet, např. při působení síly na tuhé těleso.)
Počítání s vektory Vektory můžeme násobit reálným číslem, výsledek je vektor, který má stejný směr a velikost je násobkem velikosti násobeného vektoru, Vektory můžeme navzájem sčítat (viz skládání sil). s vektory můžeme provádět vektorový a skalární součin
Trajektorie a dráha
Dělení pohybů provádíme podle trajektorie a podle průběhu
rychlosti. Podle trajektorie dělíme pohyby na přímočaré a křivočaré. Podle
průběhu rychlosti dělíme pohyby na rovnoměrné a nerovnoměrné.
Rovnoměrný přímočarý pohyb je pohyb, při kterém těleso za stejné časové intervaly urazí stejné velikosti dráhy.
Rychlost (označení v) rovnoměrného pohybu je
(vektorová) fyzikální veličina, která udává velikost dráhy (a směr
pohybu), kterou těleso urazí za jednotku času. ![]() , kde s je celková dráha, t je celková doba pohybu. Jednotka
rychlosti je m/s (metr za sekundu) nebo km/h. (Nebo také
, kde s je celková dráha, t je celková doba pohybu. Jednotka
rychlosti je m/s (metr za sekundu) nebo km/h. (Nebo také ![]() , kde
, kde ![]() s je změna
polohového vektoru a
s je změna
polohového vektoru a ![]() t je doba trvání této
změny.)
t je doba trvání této
změny.)
Průměrná rychlost nerovnoměrného pohybu je
taková rychlost rovnoměrného pohybu, při kterém by těleso urazilo tutéž dráhu za
tentýž čas, jako při pohybu nerovnoměrném. (Počítáme ji podle vztahu pro
výpočet rychlosti rovnoměrného pohybu.)
 Okamžitá rychlost tělesa je rovna rychlosti,
kterou by těleso mělo, kdyby se od daného okamžiku pohybovalo pohybem rovnoměrným
přímočarým. Okamžitá rychlost má směr tečny k trajektorii.
Okamžitá rychlost tělesa je rovna rychlosti,
kterou by těleso mělo, kdyby se od daného okamžiku pohybovalo pohybem rovnoměrným
přímočarým. Okamžitá rychlost má směr tečny k trajektorii.
Rovnoměrně zrychlený pohyb
 je zvláštní případ
nerovnoměrného pohybu, při kterém rovnoměrně s časem narůstá rychlost. Zrychlení a je přírustek rychlosti za jednotku času
(změna rychlosti za jednotku času). Přitom v0 je počáteční rychlost, s0
je počáteční dráha. Zrychlení může být i záporné (v případě rovnoměrně
zpomaleného pohybu).
je zvláštní případ
nerovnoměrného pohybu, při kterém rovnoměrně s časem narůstá rychlost. Zrychlení a je přírustek rychlosti za jednotku času
(změna rychlosti za jednotku času). Přitom v0 je počáteční rychlost, s0
je počáteční dráha. Zrychlení může být i záporné (v případě rovnoměrně
zpomaleného pohybu).
Základní vzorce:
Obecně je dráha nerovnoměrného pohybu rovna časovému integrálu rychlosti.
Volný pád je rovnoměrně zrychlený pohyb v tíhovém poli Země. Když zanedbáme odpor prostředí, pohybují se všechna tělesa volným pádem se stejným zrychlením (tíhovým zrychlením). Normální tíhové zrychlení má hodnotu g = 9,81 m/s2 a směřuje do středu Země. Tíhové zrychlení je dáno gravitační silou, má na něj vliv nadmořská výška a odstředivá síla rotačního pohybu Země.
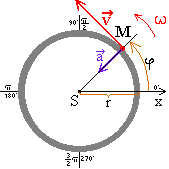 Rovnoměrný pohyb hmotného bodu po kružnici Polohu
(hmotného bodu M) určujeme pomocí poloměru otáčení r a úhlové dráhy. Úhlová
dráha
Rovnoměrný pohyb hmotného bodu po kružnici Polohu
(hmotného bodu M) určujeme pomocí poloměru otáčení r a úhlové dráhy. Úhlová
dráha ![]() je úhel, který svírá
průvodič hmotného bodu (SM) s osou x. Při rovnoměrném pohybu po kružnici roste
úhlová dráha rovnoměrně s časem
je úhel, který svírá
průvodič hmotného bodu (SM) s osou x. Při rovnoměrném pohybu po kružnici roste
úhlová dráha rovnoměrně s časem ![]() =
= ![]() .t, kde
.t, kde ![]() je úhlová rychlost. (Při rotaci tělesa kolem osy se všechny body
pohybují stejnou úhlovou rychlostí, přitom jejich okamžitá rychlost je pro každý
bod jiná.)
je úhlová rychlost. (Při rotaci tělesa kolem osy se všechny body
pohybují stejnou úhlovou rychlostí, přitom jejich okamžitá rychlost je pro každý
bod jiná.)
Veličiny pro popis pohybu po
kružnici:
úhlová dráha
úhlová rychlost
![]() =
= ![]() .t je úhel otočení
.t je úhel otočení
dostředivé zrychlení
![]() =
= ![]() = 2
= 2![]() f
je úhel (v radiánech) opsaný průvodičem hmotného bodu za
jednu sekundu
f
je úhel (v radiánech) opsaný průvodičem hmotného bodu za
jednu sekundu
ad =perioda2r =
je vektor směřující do středu otáčení (vektor rychlosti se stáčí ke středu otáčení, velikost celkové změny rychlosti za dobu jedné periody je rovna délce kružnice o poloměru velikosti vektoru rychlosti )
T =frekvencedoba jedné otáčky
f =počet otáček za jedu sekundu