Dynamika
se zabývá příčinami pohybu. Příčinou pohybu těles (nebo změny jejich
pohybu) je vzájemné působení mezi tělesy. Zavádíme vektor vzájemného
působení - sílu, označení F
Příklady 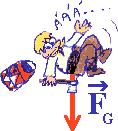 Tíhovou silou FG působí Země na
blízká tělesa a přitahuje je k zemi, (způsobuje pohyb volným pádem)
Tíhovou silou FG působí Země na
blízká tělesa a přitahuje je k zemi, (způsobuje pohyb volným pádem)
 Žhavé plyny v raketovém
motoru působí na raketu a uvádí ji do pohybu (rovnoměrně zrychleného).
Žhavé plyny v raketovém
motoru působí na raketu a uvádí ji do pohybu (rovnoměrně zrychleného).
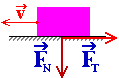
 Vozovka
působí třecí silou FT na kola automobilu a brzdí jej (způsobuje
rovnoměrně zpomalený pohyb).
Vozovka
působí třecí silou FT na kola automobilu a brzdí jej (způsobuje
rovnoměrně zpomalený pohyb).
Třecí síla
je to síla, kterou působí okolní tělesa proti směru pohybu (nebo proti
směru, kterým by se těleso pohybovalo, kdyby nepůsobilo tření).
Smykové tření
 pro třecí sílu platí:
FT = f.FN
pro třecí sílu platí:
FT = f.FN
kde FT je třecí síla, FN je tlaková síla a f je součinitel
smykového tření. Třecí síla závisí na tlakové síle (působí kolmo na
vztyčné plochy) a na kvalitě vztyčných ploch. Nezávisí na velikosti vztyčných
ploch a na rychlosti. (Při nulové rychlosti se jedná o statické tření, to je
větší, než pohybové tření.)
Skládání sil působících na hmotný bod
Působí-li více sil na hmotný
bod, můžeme je nahradit výslednicí sil, která by měla na hmotný bod stejný
účinek. Výslednici dostaneme jako vektorový součet dílčích sil.
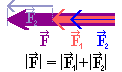 Výslednice dvou sil
působících ve stejném směru má velikost rovnu součtu velikostí obou sil a směr
shodný s oběma silami.
Výslednice dvou sil
působících ve stejném směru má velikost rovnu součtu velikostí obou sil a směr
shodný s oběma silami.
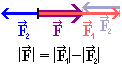 Výslednice dvou sil
působících proti sobě má velikost rovnu rozdílu velikostí obou sil a směr shodný
se směrem větší síly.
Výslednice dvou sil
působících proti sobě má velikost rovnu rozdílu velikostí obou sil a směr shodný
se směrem větší síly.
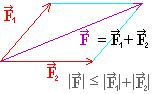 Výslednici dvou
různoběžných sil získáme doplněním na rovnoběžník sil (jako jeho
úhlopříčku).
Výslednici dvou
různoběžných sil získáme doplněním na rovnoběžník sil (jako jeho
úhlopříčku).
Pohybové zákony (Newtonovy pohybové zákony)
jsou tři základní principy, na kterých je založena klasická mechanika.
Tyto zákony platí v Newtonově absolutním prostoru a ve všech inerciálních
(setrvačných) vztažných soustavách, což jsou soustavy, které se vzhledem k
absolutnímu prostoru, a tedy i k sobě navzájem, pohybují pohybem rovnoměrným
přímočarým. Dobrým příkladem mouhou být soustavy spojené se stálicemi jako
je Slunce. Heliocentrická soustava, jejíž počátek je ve středu Slunce (přesněji v
těžišti sluneční soustavy) a jejíž osy směřují k určitým stálicím, má podle
zkušenosti vlastnosti inerciální soustavy. (Přísně vzato i stálice se pohybují.
Střed soustavy bychom pak mohli spojit s těžištěm vesmíru. Tyto úvahy by nás však
vyvedly za hranice klasické mechaniky, k úvahám o rozměrech vesmíru, jeho konečnosti
či nekonečnosti. Klasická mechanika předpokládá existenci vesmíru v klasickém
absolutním prostoru a čase. Jako by absolutní prostor existoval
mimo vesmír. Protože všechna místa absolutního prostoru jsou dostupná, mohl by
vesmír zasahovat i do těchto míst. Existoval by tedy vesmír mimo sebe ... Existoval by
vůbec? ... Samozřejmě ano, jen bychom museli uvažovat o jeho vlastnostech, které se
nedají popsat pomocí klasického prostoru a času, pomocí klasické mechaniky.)
1. pohybový zákon (zákon setrvačnosti)
Hmotný bod v inerciální
vztažné soustavě setrvá v klidu nebo pohybu rovnoměrném přímočarém, pokud
není nucen vnějšími silami tento stav změnit.
(Tato myšlenka pochází již od Galilea. Na svou dobu to byla
revoluční myšlenka, neboť se do té doby soudilo, že každý pohyb bez výjimky, a
tedy i rovnoměrný přímočarý pohyb, vyžaduje hnací sílu.)
Např. Kulička se kutálí po vodorovné desce stolu rovnoměrným
přímočarým pohybem, protože na ni působí směrem dolů tíhová síla a směrem
nahoru stejně velká síla stolní desky - výsledná síla je nulová. (Tření
zanedbáváme. Kdyby působilo tření, kulička by se pohybovala zpomaleným pohybem.)
Hybnost ozn. 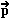
Každé těleso má určitý pohybový stav - hybnost. Chytáme-li míč, je rozdíl,
jestli chytáme pomalý míč nebo rychlý, také je rozdíl jestli se jedná o lehký
nafukovací míč, kopací míč nebo těžký medicinbal (i když se pohybují stejnou
rychlostí). Hybnost je úměrná rychlosti a hmotnosti tělesa. Závisí také na
směru - je to vektorová veličina, která má směr rychlosti
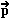 = m.
= m.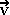 jednotkou je kg.m.s-1
jednotkou je kg.m.s-1
Hybnost soustavy hmotných bodů určíme jako vektorový součet hybností
jednotlivých hmotných bodů. (Vektorový součet provádíme stejně jaku u skládání sil.)
2. pohybový zákon (zákon síly)
Ze zákona setrvačnosti vyplývá, že pro udržení rovnoměrného přímočarého
pohybu nepotřebujeme žádnou vnější sílu. Jinými slovy: Jestliže chceme měnit
rychlost pohybu nebo jeho směr, musíme na těleso působit vnější silou. Vnější
síla přímo souvisí se změnou pohybového stavu tělesa (se změnou hybnosti
tělesa, se změnou směru nebo velikosti vektoru hybnosti). Změna hybnosti je tím
větší, čím větší je působící síla a tím větší, čím je větší doba
působení síly.
Platí:
m.v = F.t
získaná hybnost se rovná impulzu
síly
F.t = m.v /:t
F = m.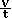
F = m.a
Jestliže na těleso hmotnosti m působí síla 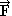 , pak mu udělí zrychlení
, pak mu udělí zrychlení 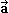 takové, že
platí:
takové, že
platí: 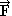 = m.
= m.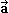 (zrychlení má směr síly).
(zrychlení má směr síly).
nebo:
Výsledná působící síla je rovna časové změně hybnosti
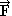 =
= 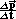
Jednotkou síly je newton
Příklady:
Jestliže má automobil o hmotnosti 1000 kg zrychlit z 0 na 100 km/h (přibližně 30 m/s)
za 5 sekund, musí motor působit silou 1000.30/5 = 6 000 N (dá se spočíst, že to
odpovídá výkonu motoru 90 kW - zanedbáme-li odpor vzduchu)
Jestliže budeme vozík o hmotnosti 100 kg a rychlosti 2 m/s brzdit silou 50 N,
zastavíme jej za dobu 4 sekundy. (m.v=F.t, 100.2/50=4 s)
Jestliže na železniční vagón budeme působit známou silou a
změříme dosažené zrychlení, můžeme spočíst hmotnost vagónu m = F/a Takovéto
hmotnosti říkáme hmotnost setrvačná. Určíme-li hmotnost vážením - pomocí
gravitační síly, hovoříme o hmotnosti gravitační.
(Protože jsou setrvačná i gravitační hmotnost tak blízké
veličiny, projevující se různými způsoby: setrvačností a vzájemným
přitahováním, volíme pro obě veličiny stejnou jednotku. V praxi nás obvykle ani
nenapadne, abychom obě hmotnosti rozlišovali.)
3. pohybový zákon, zákon vzájemného působení (zákon akce a reakce)
Dvě tělesa na sebe působí silami stejně velikými a opačně
orientovanými 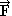 1 = -
1 = -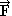 2
2
 Při přetahování budou oba
siloměry ukazovat stejně velkou sílu.
Při přetahování budou oba
siloměry ukazovat stejně velkou sílu.
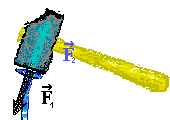 Při úderu kladiva na
hřebík zarazí kladivo hřebík silou F1 stejně velkou jako je síla F2,
kterou hřebík zastaví letící kladivo.
Při úderu kladiva na
hřebík zarazí kladivo hřebík silou F1 stejně velkou jako je síla F2,
kterou hřebík zastaví letící kladivo.
Zákon zachování hybnosti
Součet hybností těles izolované soustavy je stálý
např.:
Součet hybností těles před srážkou je roven součtu hybností těles po
srážce.
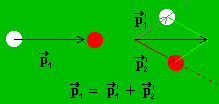 Hybnost kulečníkových
koulí před srážkou je
Hybnost kulečníkových
koulí před srážkou je 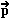 1
(červená koule je před srážkou v klidu) a hybnosti po srážce jsou
1
(červená koule je před srážkou v klidu) a hybnosti po srážce jsou 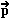 1' a
1' a 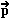 2'.>
2'.>
Před výstřelem pušky je hybnost pušky a střely nulová, po výstřelu je
vektorový součet hybností nulový, velikost hybnosti střely je rovna velikosti
hybnosti pušky. (Hybnosti mají opačný směr, při výstřelu dojde k tzv. zpětnému
rázu.)
Po nepružné srážce (po srážce se tělesa spojí) se tělesa pohybují společnou
rychlostí a hybnost takto vzniklého tělesa je rovna součtu hybností těles před
srážkou.
Reaktivní motor rakety pracuje tak, že hybnost rakety a paliva je nulová. Jestliže
začnou z rakety tryskat žhavé plyny obrovskou rychlostí, mají i při malé hmotnosti
vysokou hybnost. Protože musí být celková hybnost nulová, získá raketa hybnost
stejně velikou v opačném směru.
(Problém pohybu raket může být mnohem komplikovanější a také
zajímavější v okamžiku, kdy začneme uvažovat změnu hmotnosti rakety v důsledku
ubývání paliva.)
Galileův pincip relativity
Zákony mechaniky jsou stejné ve všech inerciálních vztažných soustavách.
např.:
Volně puštěné těleso ve stojícím vlaku padá stejně jako ve vlaku jedoucím
stálou rychlostí po přímé trati (samozřejmě vzhledem k pozorovateli spojenému s
tímto vlakem).
V uzavřené kajutě lodi nemůžeme zjistit, zda se loď pohybuje, nebo je v
klidu. Pohyb určujeme jen relativně.
V klasické mechanice platí Galileovo skládání rychlostí. (Jestliže indián
jedoucí na koni vystřelí šíp ve směru jízdy, bude rychlost šípu vzhledem k zemi
rovna součtu rychlosti šípu vzhledem k indiánovi a rychlosti koně vzhledem k zemi.
Šíp tak má různé rychlosti vzhledem k různým vztažným soustavám)
Neinerciální vztažná soustava
Je soustava, která se pohybuje se zrychlením vzhledem k některé inerciální vztažné soustavě.
např.:
Soustava spojená s autobusem projíždějícím zatáčkou (soustava s dostředivým
zrychlením).
Soustava spojená s brzdícím/rozjíždějícím se autobusem.
Jestliže stojíme volně ("bez držení") v autobusu, který se rozjíždí
se zrychlením 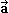 , začne
na nás působit síla směrem k zádi autobusu. Této síle říkáme setrvačná síla.
, začne
na nás působit síla směrem k zádi autobusu. Této síle říkáme setrvačná síla.
V neinerciální vztažné soustavě, která se pohybuje se zrychlením 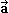 , působí na všechna tělesa
(fiktivní) setrvačná síla F, která působí proti zrychlení
soustavy a má velikost:
, působí na všechna tělesa
(fiktivní) setrvačná síla F, která působí proti zrychlení
soustavy a má velikost:
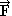 s
= -m.
s
= -m.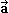
např.: volně položený míč na podlaze takového autobusu se
začne (v důsledku působení setrvačné síly) pohybovat se zrychlením -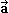 vzhledem k autobusu (vzhledem
k zemi bude stát na místě).
vzhledem k autobusu (vzhledem
k zemi bude stát na místě).
Znáte trik s ubrusem? ... To si
na stůl prostřete ubrus. Na ubrus rozestavíte babiččin porcelánový servis,
maminčino broušené sklo, přičemž sklenice můžete pro lepší efekt stavět i do
pyramidy. Potom pozvete co největší publikum, ubrus uchopíte pevně za okraj a silně
jím trhnete, až se smekne se stolu. V případě, že nádobí zůstane neporušeně
stát na holém stole, můžete užaslému publiku vysvětlit, že přeci sklenice na
stůl stáhla setrvačná síla. V opačném případě se nenechte odradit, ukliďte
střepy a celý pokus zopakujte s vysvětlením, že musíte použít větší zrychlení
ubrusu, aby mohla být třecí síla vzhledem k setrvačné zanedbána.
Ohraničená platnost zákonů
klasické mechaniky
Zákony klasické mechaniky přesně fungují v situacích, se kterými se
v přírodě běžně setkáváme. Současně si však musíme uvědomit, že
příroda nemusí mít nám známé vlastnosti vždy! V situacích, do kterých se
běžně nedostáváme, nebo nemůžeme dostat, musíme předpokládat vlastnosti
přírody, které nejsou běžné. Musíme se smířit s tím, že existují
vlastnosti přírody, které nejsou běžným způsobem pochopitelné. (Sousloví
"běžným způsobem" bychom zde mohli často nahradit souslovím "selským
rozumem".)
Které situace máme zahrnout mezi běžné? Všechny ty, pro které jsou splněny
předpoklady klasické fyziky - existence absolutního prostoru a absolutního času, děje probíhají nízkými rychlostmi (ve
srovnání s rychlostí světla) a události probíhají v rozměrech velkých ve
srovnání s rozměry atomů.
Pokud se budeme pohybovat rychlostmi do 80 km/s (což je rychlost 10 krát
vyžší než první kosmická
rychlost), budou relativní odchylky od klasické mechaniky patrné až na 8. des.
místě, tedy prakticky neměřitelné. (Např. hodinky, které by měřily s takovou
přesností, by musely odměřit jeden rok s přesností na jednu sekundu a tachometr s
takovou přesností by musel měřit vzdálenost 30 km s přesností na jeden milimetr!)
Slovo práce může mít celou řadu významů (tělesná, duševní, výtvarná,
práce jako zaměstnání... Nejblíž k fyzikálnímu významu slova práce má práce
tělesná - proto někdy také fyzická. Pozor! Když přenášíme rovnoměrným pohybem
těžký balík, nekonáme fyzikální práci! I když hovorově řekneme, že pracujeme.)
Mechanická práce
má ve fyzice přesně stanovený význam. Týká se děje, při kterém působí síla
F po dráze s ve směru posunutí. Práce je
fyzikální veličina, označení W, jednotkou je joule J a platí:
Síla F působící ve směru posunutí o velikosti s vykoná práci W takovou,
že platí:
W = F . s
Práci může konat i síla, která nemá směr posunutí. Když ji rozložíme do dvou
směrů, kolmého na směr posunutí (tato složka nekoná práci) a rovnoběžného se
směrem posunutí (tato složka koná práci podle výše uvedené definice), platí pro
práci vztah:
W = F . s . cos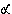

kde 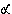 je úhel
mezi působící silou a směrem posunutí.
je úhel
mezi působící silou a směrem posunutí.
Výkon označení P,
jedotka W (watt)
je fyzikální veličina, která udává množství práce vykonané za
jednotku času. Platí:
P = 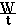
kde W je práce vykonaná za dobu t.
Kinetická energie hmotného bodu
označení Ek , jednotka joule, vztah:
Ek = 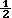 m.v2
m.v2
kde m je hmotnost tělesa a v jeho rychlost. Jestliže pohybující se těleso narazí
na překážku, koná při nárazu práci (např. se deformuje). Má tedy energii. Ta je závislá na pohybovém
stavu tělesa. Proto jí říkáme kinetická (pohybová).
K odvození vztahu pro kinetickou energii: Jestliže síla F
působbí na volné těleso o hmotnosti m po dráze s,
vykoná na něm práci W, která se přemění na kinetickou energii.
Naopak - při zastavování tělesa (např. brzdnou silou) se kinetická energie
přemění v práci třecích sil a platí:
Ek = W = F.s = m.a.s = m.a. 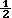 a.t2 = m.
a.t2 = m.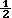 (
(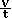 )2.t2
=
)2.t2
= 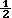 m.v2
m.v2
Další formou energie je:
Potenciální energie
označení Ep, jednotka joule. Jestliže napínáme pružinu, zvedáme závaží,
vzdalujeme magnety, konáme práci na soustavě, ve které se mění poloha těles. Návratem
těles do původní polohy může soustava konat práci. Říkáme, že má polohovou
(potenciální) energii.
Častým příkladem potenciální energie je energie v tíhovém poli Země. Tedy
potenciální energie soustavy těleso - Země.
Potenciální tíhová energie
Zvedáme-li závaží kyvadlových hodin, konáme práci proti tíhové síle závaží.
Závaží získá potenciální (polohovou) energii vzhledem k Zemi. Při obráceném ději
může závaží konat práci. Obecně platí:
Ep = W = F.h = m.g.h
Ep = mgh
kde m je hmotnost tělesa, h je výška a g je tíhové zrychlení.
Přesněji:
W = 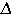 Ep = mg
Ep = mg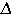 h
h
kde práce W se projeví jako změna potenciální energie
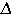 Ep = Ep2 - Ep1
a namísto výšky h dosadíme výškový rozdíl
Ep = Ep2 - Ep1
a namísto výšky h dosadíme výškový rozdíl
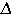 h = h2 -
h1
h = h2 -
h1
Do výšky h = 0 klademe hladinu nulové potenciální energie. (Tuto hladinu
spojujeme obvykle s povrchem země, hladinou moře, rovinou podlahy nebo s místem nejnižší
potenciální energie pro daný příklad.)
Jestliže se dostane těleso pod úroveň hladiny nulové potenciální energie, může
být potenciální energie i záporná.
Změna potenciální energienení není závislá na tvaru dráhy, kterou těleso prošlo,
pouze na počáteční a konečné výšce tělesa nad zemí. (To nám umožňuje počítat
potenciální energii i při velmi složitých pohybech. Např pád listu papíru, pohyb
kyvadla po kružnici ...)
Mechanická energie
Celkovou mechanickou energii soustavy zavádíme jako součet celkové kionetické
energie a součet celkové potenciální energie všech částic soustavy.
E = Ek + Ep
Vztahy mezi těmito formami energie si můžeme ukázat na příkladu volného pádu míče
(zanedbáme odpor prostředí). Na počátku volného pádu má míč potenciální
energii Ep = mgh a nulovou kinetickou energii. Tíhová síla postupně zvyšuje
jeho kinetickou energii a ve výšce h = 0 platí:
Ep = 0, Ek = 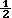 m.v2 =
m.v2 = 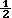 m.(g.t)2
= m.g
m.(g.t)2
= m.g 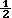 .g.t2 = m.g.h
.g.t2 = m.g.h
Tedy došlo k přeměně potenciální energie na kinetickou tak, že úbytek potenciální
energie se rovná přírustku kinetické energie. Za předpokladu, že do soustavy nebudou
zasahovat vnější vlivy, můžeme vyslovit důležitý fyzikální zákon:
Zákon zachování mechanické energie
V izolované soustavě je celková mechanická energie stálá.
Ek + Ep = konst
Volný pád míče můžeme sledovat dál. V okamžiku, kdy se dotkne země,
začne se deformovat. Kinetická energie se přemění v práci deformující síly. Předpokládáme-li
dokonale pružný míč, projeví se tato práce v nárustu potenciální energie zmáčknutého
míče. Při maximálním zmáčknutí se míč zastaví, kinetická energie bude nulová,
potenciální energie míče bude opět rovna mgh. Síly pružnosti míče opět míč
vymrští, potenciální energie se sníží a naroste opět kinetická energie, která se
se stoupající výškou bude snižovat a míč bude opět nabývat potenciální
energii, až se zastaví v maximální výšce h. V případě, že nebude působit odppor
prostředí a srážka míče se zemí bude dokonale pružná, bude se děj neustále
opakovat. (V reálné skutečnosti se míč po čase zastaví a jeho energie se přemění
v jiné formy. Přesným měřením bychom zjistili zvýšení teploty míče a jeho okolí.)
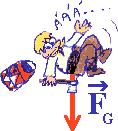 Tíhovou silou FG působí Země na
blízká tělesa a přitahuje je k zemi, (způsobuje pohyb volným pádem)
Tíhovou silou FG působí Země na
blízká tělesa a přitahuje je k zemi, (způsobuje pohyb volným pádem) Žhavé plyny v raketovém
motoru působí na raketu a uvádí ji do pohybu (rovnoměrně zrychleného).
Žhavé plyny v raketovém
motoru působí na raketu a uvádí ji do pohybu (rovnoměrně zrychleného). Vozovka
působí třecí silou FT na kola automobilu a brzdí jej (způsobuje
rovnoměrně zpomalený pohyb).
Vozovka
působí třecí silou FT na kola automobilu a brzdí jej (způsobuje
rovnoměrně zpomalený pohyb). pro třecí sílu platí:
FT = f.FN
pro třecí sílu platí:
FT = f.FN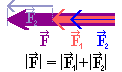 Výslednice dvou sil
působících ve stejném směru má velikost rovnu součtu velikostí obou sil a směr
shodný s oběma silami.
Výslednice dvou sil
působících ve stejném směru má velikost rovnu součtu velikostí obou sil a směr
shodný s oběma silami.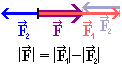 Výslednice dvou sil
působících proti sobě má velikost rovnu rozdílu velikostí obou sil a směr shodný
se směrem větší síly.
Výslednice dvou sil
působících proti sobě má velikost rovnu rozdílu velikostí obou sil a směr shodný
se směrem větší síly. Výslednici dvou
různoběžných sil získáme doplněním na rovnoběžník sil (jako jeho
úhlopříčku).
Výslednici dvou
různoběžných sil získáme doplněním na rovnoběžník sil (jako jeho
úhlopříčku). Při přetahování budou oba
siloměry ukazovat stejně velkou sílu.
Při přetahování budou oba
siloměry ukazovat stejně velkou sílu.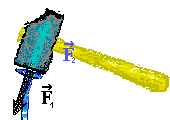 Při úderu kladiva na
hřebík zarazí kladivo hřebík silou F1 stejně velkou jako je síla F2,
kterou hřebík zastaví letící kladivo.
Při úderu kladiva na
hřebík zarazí kladivo hřebík silou F1 stejně velkou jako je síla F2,
kterou hřebík zastaví letící kladivo. Hybnost kulečníkových
koulí před srážkou je
Hybnost kulečníkových
koulí před srážkou je 